人工智能-第一周周报

Yaosanqi1372025年5月3日大约 12 分钟

人工智能-第一周周报

本周任务：https://gitee.com/gaopursuit/ouc-dl/blob/master/week01.md

概述

这周主要先学一些深度学习的一些基础知识，认识一些基础概念和深度学习的一些底层逻辑

代码环境搭建

这不爱特服务器最近上新了一套新设备嘛，我整了台小主机，里面装了两块 v100 16G ，而主板支持 NVlink ，跑 LLM 的时候可把我爽疯了（缺点就是散热噪音有点太大了，开学以后再换新风扇吧）

所以我决定，不使用 Colab 了，自己搭 Jupyter Notebook ，Colab 那玩意我上计导的时候就用吐了，不想再用它了

对于这个，有一个现成的 docker 镜像，大家想要自己搭的可以试试

进去以后，发现没有中文，字体不好看，主题难看。

可以参考以下文章自己调，总之调完以后挺爽的

切换主题、修改字体、中文包

其他的什么，比如 UI 、终端字体、字体大小什么的，Jupyter 设置里面都有，可以自己摸索一下

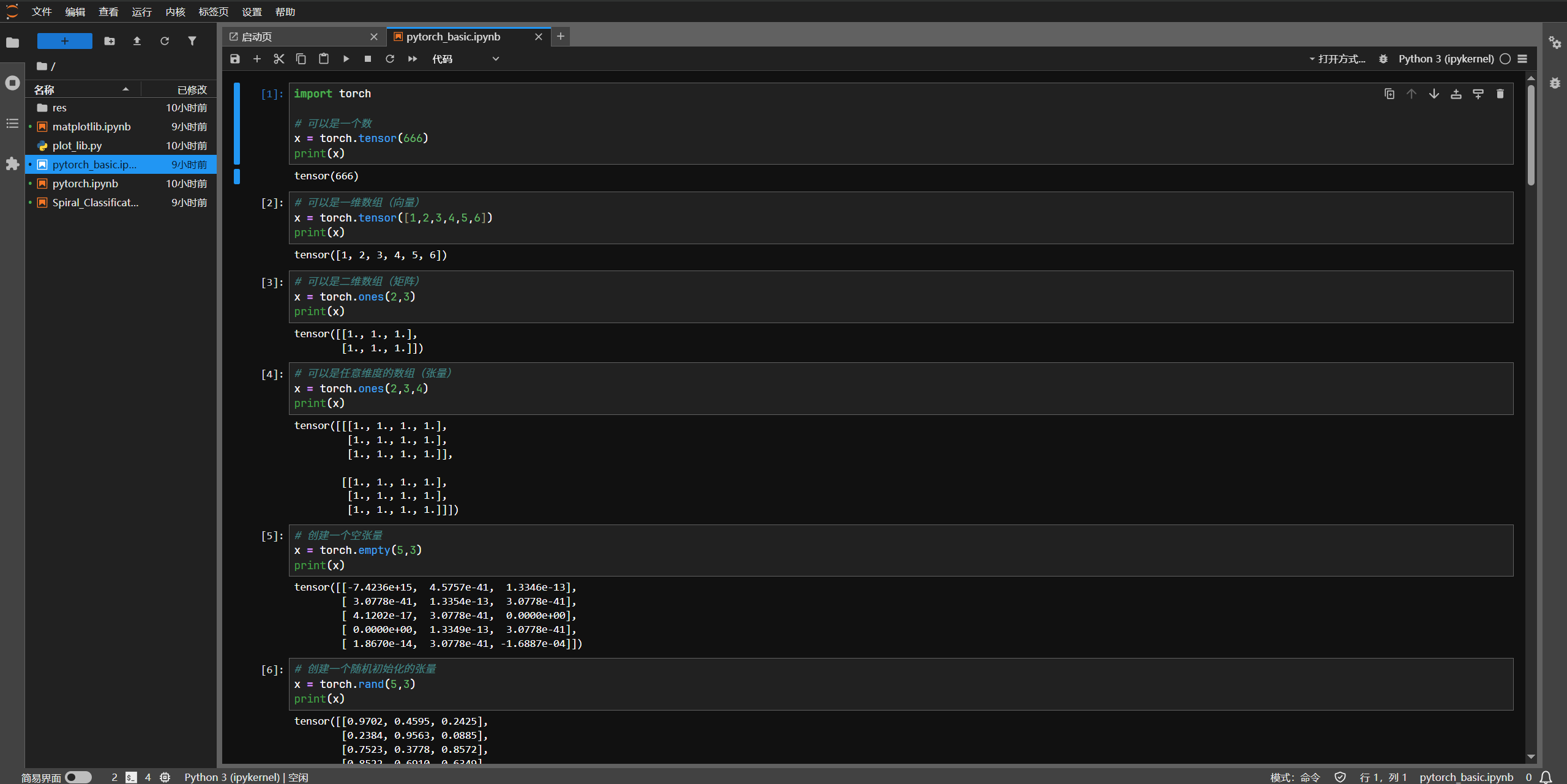
pytorch 基础练习

pytorch 是人工智能常用的一个 python 框架，是人工智能学习的基础，这周我们先学习 pytorch 中张量的创建和操作

这里由于条目太多，我就单放截图了

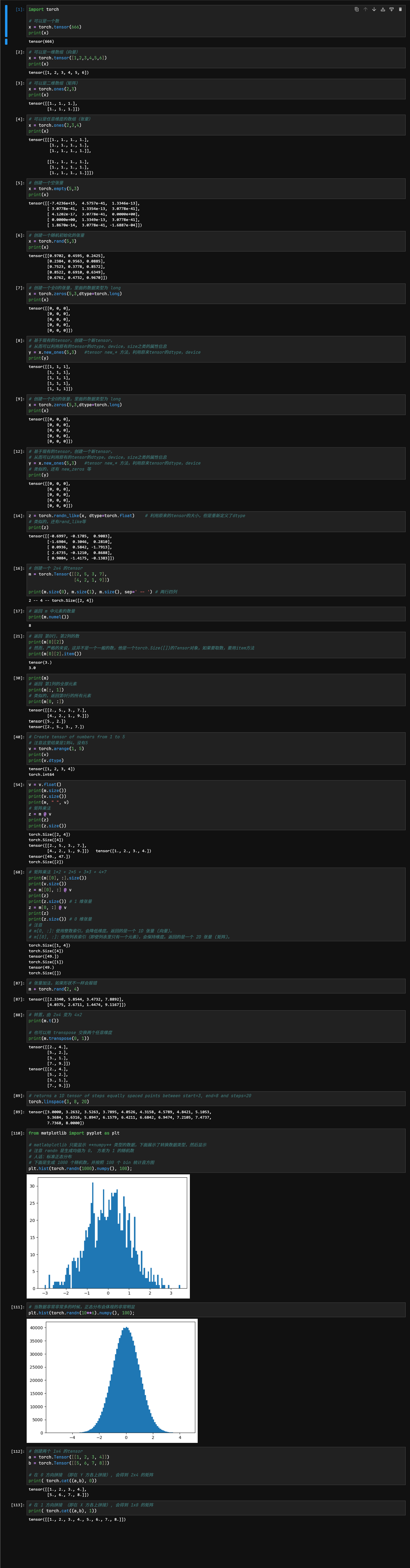
这里面的坑有点多，这里需要注意几点：

第一，直接使用索引获取张量中的某个元素，得到的仍然是张量，而不是一个常规的 python 数字，比如

m = torch.Tensor([[2, 5, 3, 7],
                  [4, 2, 1, 9]])

print(m[0][2])
# 这里输出的是 tensor(3.) ，是一个零维张量

print(m[0][2].item())
# 这里输出的才是正经的 3.0 ，是常规的 python 数字

第二，小心切片

m = torch.Tensor([[2, 5, 3, 7],
                  [4, 2, 1, 9]])
                  
# m[[0], :] 和 m[0, :] ，你觉得这两个一样吗？
# 🤔，看上去就是一样的，但是维度不同了

z = m[[0], :]
print(z)
print(z.size()) # 显示 torch.Size([1])，这是一维张量，人话就是这样做会保持张量的维度
z = m[0, :]
print(z)
print(z.size()) # 显示 torch.Size([])，这是零维张量，人话就是这样张量会少一个维度

第三，要注意张量元素的数据类型

# 假如 m 和 n 在数学上是可以做矩阵乘法的，但是他们的 dtype 不一样，比如 m 的元素都是 float ，n 的都是 int
# 现在做乘法
m @ n

# 这样会报错，所以在这么做之前，要先给张量统一元素的数据类型
n.float()

# 现在这么做就可以了
m @ n

第四，最新的 MatlabPlotLib 目前已经不需要手动将 torch 对象换成 numpy 对象了，它自己会换的，你只管用就好了

里面还留了一个问题叻，transpose() 方法是啥？

讲人话，这玩意就是交换张量的两个维度，图中使用了 transpose(0, 1) 就是交换张量的第零维（行）和第一维（列），等价于 t() 方法，矩阵转置方法

差不多就是这些了，如果想要学习更多，可以参考 pytorch 文档

螺旋数据分类

本次代码中将解决 spiral classification 问题

讲人话就是一大坨螺旋状分布的数据，你咋用深度学习的方法给他分开

那我们先把代码丢到我们的 Jupyter 里面看看效果吧

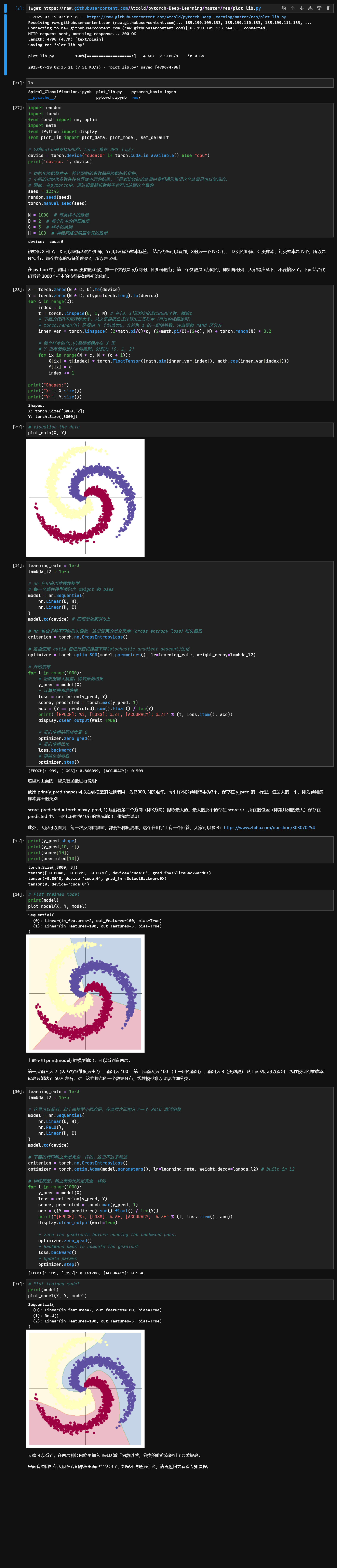
不得不说，v100 的 AI 性能确实很有性价比

回归正题，先说一个问题，就是如果你是自己搭的 Notebook ，你是运行不了程序的，原因是 plot_lib.py 里面用到了一张照片，但是你的本地环境里面并没有

只需要再用 wget 拿一下那个资源：https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/ziegler.png

然后在工作区文件夹里面创建一个 res 文件夹，把照片丢里面就可以了

来讲讲这个实验

1. 为什么两种回归方法得到的结果截然不同？

首先我们来看看两个结果

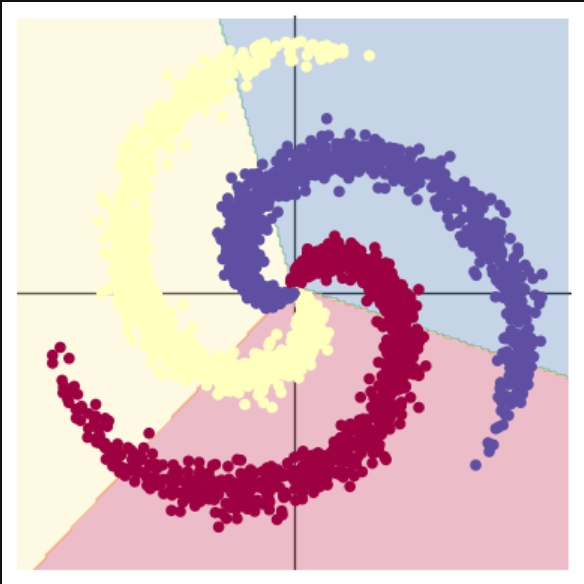
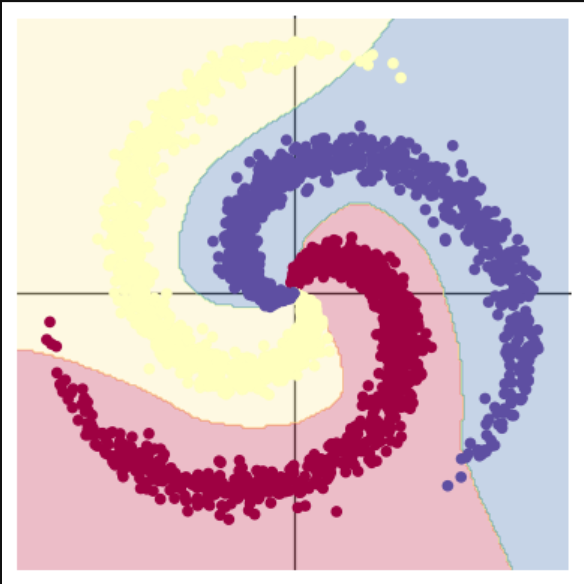
很明显的区别是前者的分割线是直线，后者是曲线，而且是能够几乎完美划分三种数据的曲线

其实两者的代码差不多，但是最关键的一点是啥？来看看

# 前者创建线性模型的代码：
model = nn.Sequential(
    nn.Linear(D, H),
    nn.Linear(H, C)
)

# 后者创建线性模型的代码：
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)

区别仅仅在于，后者用了一个 ReLU 激活函数

那 ReLU 激活函数是何方神圣？为什么有这么大的魔力？首先来认识认识激活函数是什么？我这里有两张图帮助理解

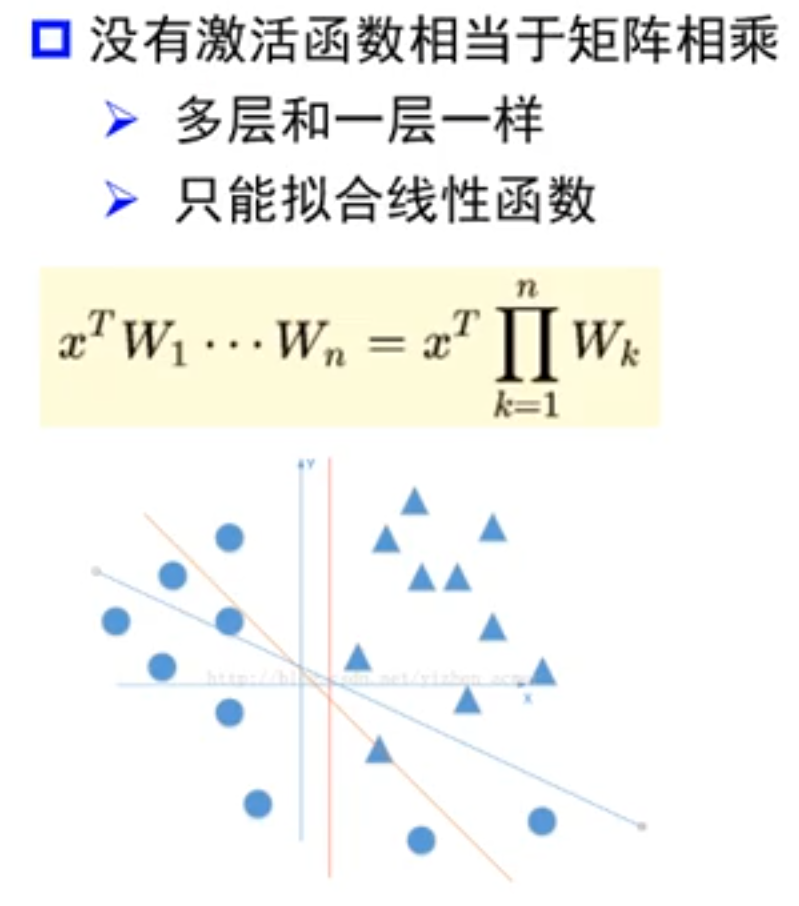
我们都知道，人工智能的底层简单的说是矩阵可以理解为一大堆线性方程组列在一起，那如果你只有矩阵，乘来乘去，加来减去，还是矩阵，那不就只能拟合直线了呗，再专业一些，神经网络中每一层的核心计算都是一次线性变换

而多次线性变换的堆叠，其结果仍然等价于一次单独的线性变换。比如 W2 * (W1 * x + b1) + b2 可以被简化成一个新的 W' * x + b'。因此，一个没有激活函数的网络，其表达能力和一个单层网络没有区别

而在每一层神经网络加上激活函数，“神经元”在收到“刺激”的时候，应答就不会那么死板，而是能够做到在达到收到某种程度的“刺激”再激活，甚至应该是怎么样的激活

这似乎不能够解释它为啥能把线性变成非线性，从数学上说，感知器的工作步骤是给每一个输入的值乘一个权重，之后也可能会再加一个偏置值，形如：

权重 * 数据值 + 偏置值

之后求和再过一遍激活函数，激活函数可不一定是线性的，它可能是一个曲线（比如 Sigmoid 、tanh 激活函数）或者是直线，但是是分段直线（比如 ReLU 、Leaky ReLU 激活函数）

我们就会得到

结果 = 激活函数( $\sum$ 权重 * 数据值 + 偏置值)

那这好像也不是很线性啊，也不可能拟合成图中那么夸张的吧？

别急，之后，这个结果会传递到下一层神经网络中，以此类推，我们就会得到这样一个函数：

结果 = 激活函数(激活函数(激活函数(...)))

你把这个函数一复合，就会得到一个很复杂的函数，大概率不是线性的，我们就可以得到非线性的结果了

如果这还理解不了？那你可以想想一下打印在纸上的数据，不要想数据，把这张纸拿起来，揉几下，直到这些数据点用肉眼直接看上去能够被一条线分割

因此，激活函数的另外一层理解，是每一层非线性激活都会对数据空间进行一次“扭曲”或“折叠”

2. 还能再厉害吗？

当然可以，我们注意到这里我们定义了 4 个常量

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量

大可修改一些数据再来跑跑看看，如果效果不好，可以尝试增加迭代次数或换做其他激活函数看看效果

问题解答

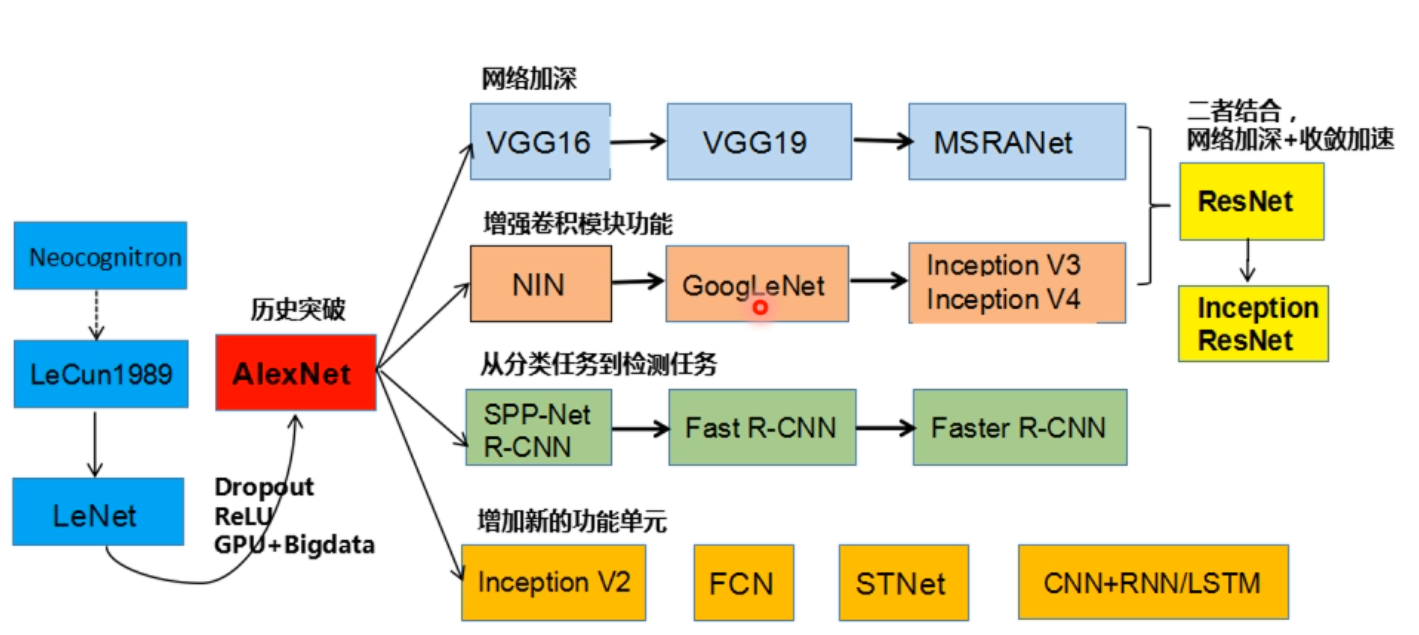
Q: AlexNet 有哪些特点？为什么可以⽐ LeNet 取得更好的性能？

A: 我们来看一张图吧

首先，AlexNet 使用了 ReLU 作为激活函数，比起 LeNet 使用的 Sigmoid 和 tanh 性能更佳，求导也更简单，也不会出现梯度消失这些问题，收敛也更加快速
基于上句话，这也就决定了 AlexNet 相比于 LeNet，能够将神经网络训练的更深，也就能够得到更好的结果
其次，AlexNet 使用了 Dropout 来防止过拟合，这样网络就不会过于依赖某些神经元，让所有神经元都能够好好工作，不要摸鱼，从而减少过拟合现象
不仅如此，AlexNet 甚至还会自己给自己造训练数据，通过将已有数据进行变换来达到自己造数据的目的，以减少过拟合现象并增强了模型的泛化能力，类似人类的“举一反三”
AlexNet 还能利用多 GPU ，实现了多块 GPU 并行训练，大大优化了训练
事实上，AlexNet 还有很多方面超越了 LeNet，这里就不再赘述了

Q: 激活函数有哪些作⽤？

A: 从上文我们知道，最直接的作用就是实现了非线性回归
而且，激活函数还能控制输出值的范围，让输出不会太大，也不会太小，充当阀门的作用
在第一问中，我们知道，选择了好的激活函数，一定程度上可以避免梯度消失、收敛速度太慢、训练不充分等问题

Q: 梯度消失现象是什么？

A: 首先我们要知道，在神经网络学习过程中，还有一个叫反向传递的过程来调整内部参数，本质上是在计算损失函数对网络参数的梯度
简单的来说，反向传递类似你考试并对完答案过后，一个复盘的过程
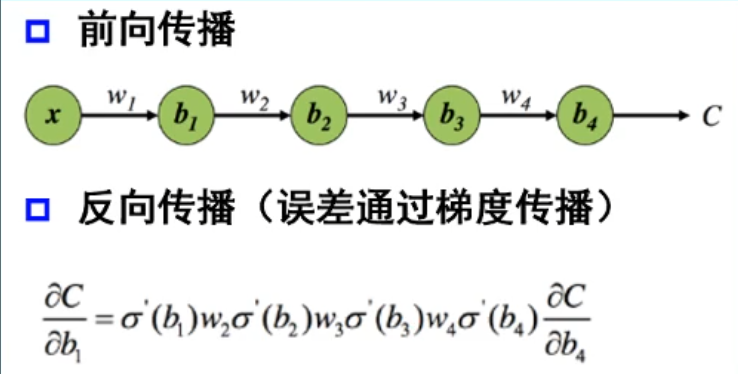
当然，你复盘的过程自然要从尾到头反着倒退一遍才能知道自己错哪了，这就是反向传递。在数学上，深度学习的反向传递的表达式看起来是这样的：

其中， $\sigma'$ 表示激活函数的导数，整体就是这样一个链式求导的一个公式，来得出每一步的梯度值，如果我们选择了类似 Sigmoid 这样的激活函数时，发现它的导数都很小
同时看到，图中的 $w$ 也会影响梯度计算的结果，这个 $w$ 是神经网络的权重值，因此权重值选取不当也可能会造成梯度消失的情况
那么从这里可以看出，如果神经网络越深，那么计算出来的梯度值也就会越接近 0 ，这就是梯度消失现象
如果出现梯度消失现象，就人类而言，你如果找不到错在哪，那么你的学习进度就会停滞，那么深度学习也是如此，模型的学习可能会减缓甚至停滞，也就无法训练更深的神经网络，模型性能就会很差
想要解决梯度消失现象，最简单的方法就是换一个激活函数，比如 ReLU 激活函数，当然还有其他一些方法，这里就不再多说了

Q: 神经⽹络是更宽好还是更深好？

先说结论，更深更好
有实验指出，同样的神经网络节点数，构建的更深比构建的更宽的网络有更强的网络表示能力，错误率更低
深度和宽度对整个函数的复杂程度贡献是不同的，深度的贡献是指数增长的，而宽度只是线性增长的，可以参考下面这个公式
$FC = \prod_{l=1}^{d} (\alpha_{l} \cdot \theta_{l})^{\beta_{l}}$
其中 $\alpha_l$ 是宽度对函数复杂度的贡献， $\beta_l$ 是深度对函数复杂度的贡献，显然，神经网络是更深更好的

Q: 为什么要使⽤Softmax？

先来解释一下 Softmax 的基本功能，它能够将一个模型的原始输出变换成一个概率分布，取值范围在 0 到 1 之间，结果的总和等于 1 ，也就是 100%
如果单看原始输出，那你可能不知道这一大堆数是啥意思，比如大模型输出一个很抽象的结果：
狗: 523.42354，猫: 123.1652，鸟: 56.51243
这谁知道这什么意思？但是如果在输出层套上一个 Softmax 函数，结果可能会变成
狗: 0.8，猫: 0.1，鸟: 0.1
我们就能够直观理解为大模型识别出狗的概率是 80% 猫和鸟是 10% ，能够得到一个解释性强的结果
通过 Softmax ，在处理多类别的分类任务时，我们就能通过每个类别的概率，得到最可能、最符合要求的结果

Q: SGD 和 Adam 哪个更有效？

一般是 Adam 更加有效
先来说说这两个是什么东西，这两个是优化器，用来优化梯度下降
梯度下降，就好比一个人从山上跑到山谷的最低点，用最快的速度跑到最低的地方
而 SGD 和 Adam 就是这样一个优化器，让这个人尽快下山，而且要下到最低点
其中，SGD 全名叫 Stochastic Gradient Descent 翻译作随机梯度下降
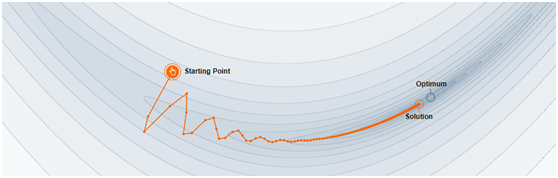
它的路径大概是这样的

来自 https://distill.pub/2017/momentum/
它通过引入动量的概念，类似将人比作一个滚石，自然能够快速下山
但这也引入一个问题，就是 SGD 有可能会陷入局部最优而不是全局最优
而且这也导致 SDG 对初始化和学习率比较敏感
于是 Adam 就对 SDG 很多缺点进行了优化，跟 SDG 相比，Adam 对内存的需求更少，对初始学习率的要求也不会很高
通过解决这些问题，Adam 很适合应用在数据、参数规模巨大的工作当中
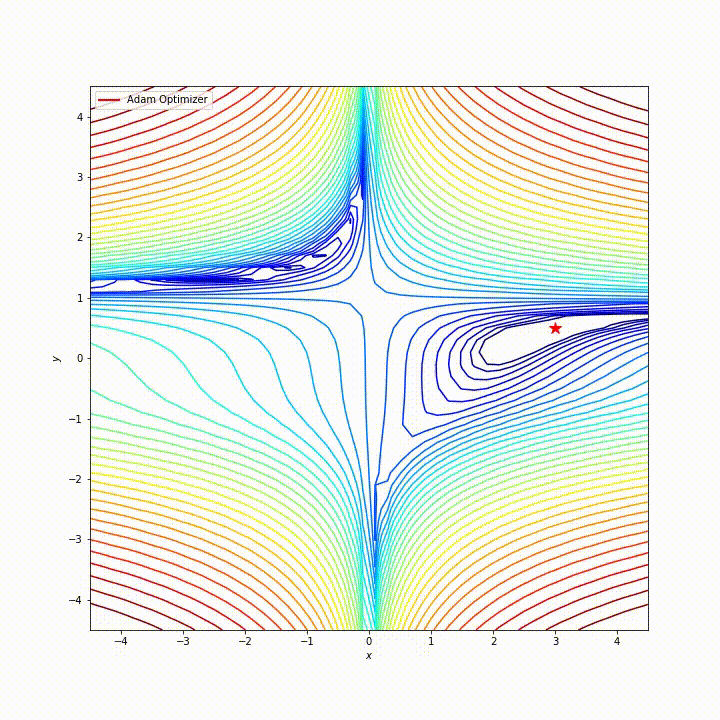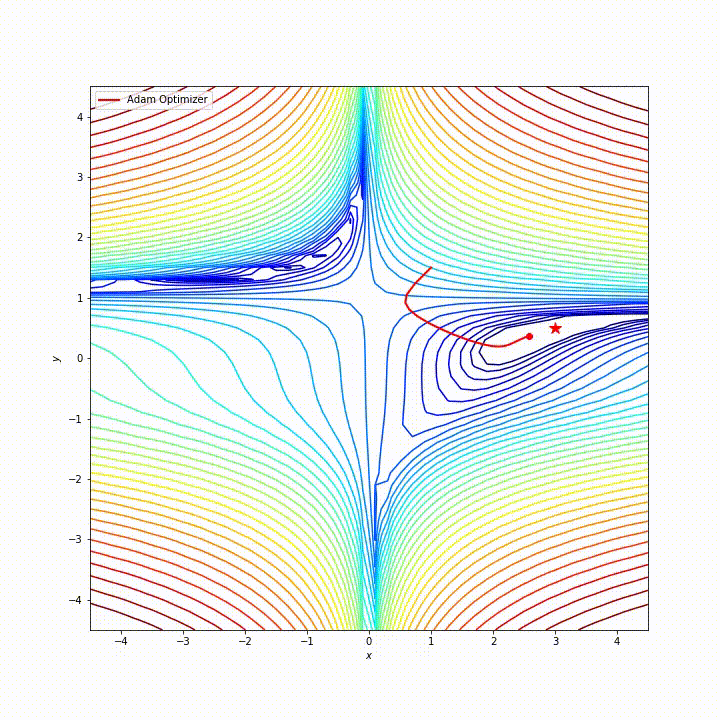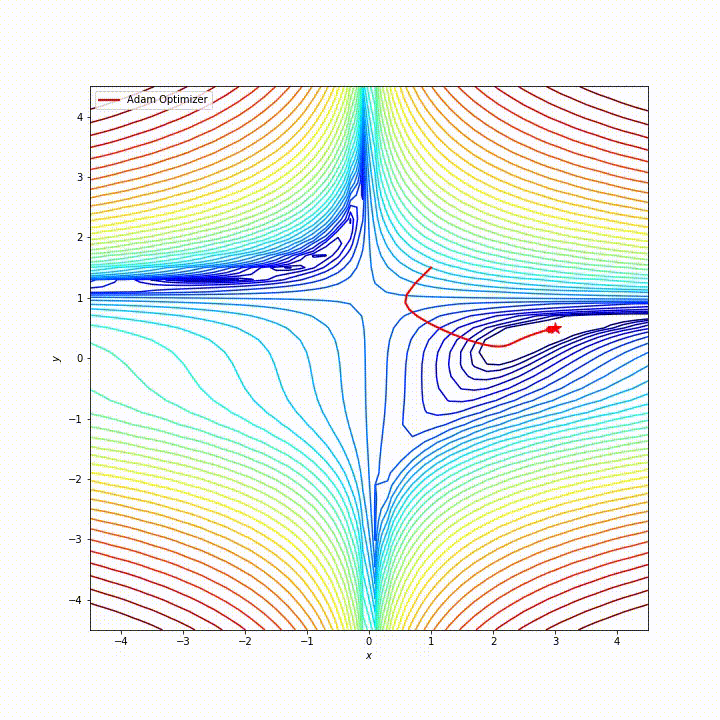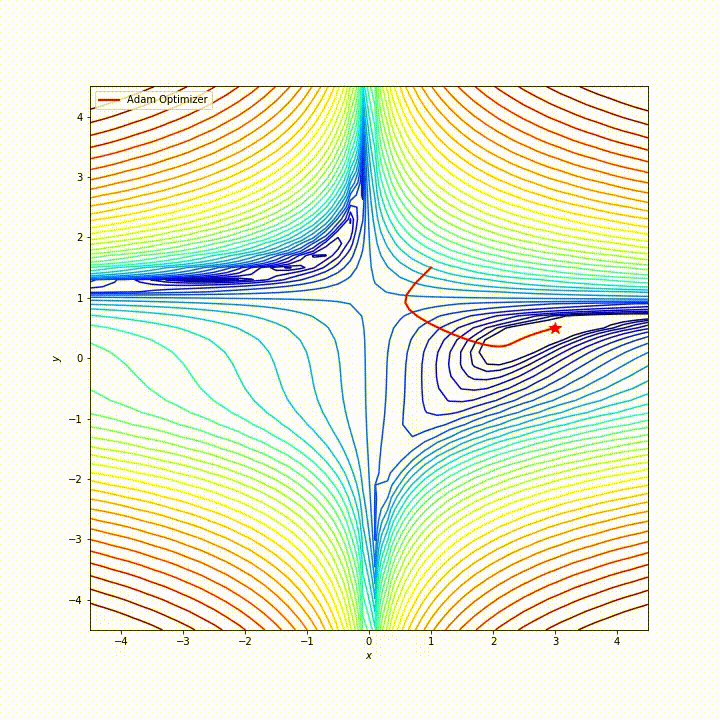
综合来看，Adam 在很多情况下，都是非常优秀的优化器，它的路径大致是这样的：

来自 https://zhuanlan.zhihu.com/p/32698042
但是 Adam 也有一些缺点，比如有报告指出，Adam 的自适应学习率机制在训练后期可能会导致学习率过小，从而错过最优解
更详细的解读可以看这篇文章：https://zhuanlan.zhihu.com/p/32698042

贡献者

Yaosanqi137