运动学基础

基础概念

提示

最好自己上完课了再来看，这样体验更佳

位矢

定义: 从原点O到P点的有向线段 $\vec{OP}$ = $\bf{r}$ 来表示，矢量$\bf{r}$称为位置矢量

在直角坐标系中，位矢$\bf{r}$可以表示成

$\bf{r} = x\bf{i} + y\bf{j} + z\bf{k}$

其中，$\bf{i}、\bf{j}、\bf{k}$ 分别是 x y z 轴正方向的单位矢量，位矢$\bf{r}$的大小为

$|\bf{r}| = \sqrt{x^2 + y^2 +z^2}$

方向余弦为

$\cos{α} = \frac{x}{r}, \cos{β} = \frac{y}{r}, \cos{γ} = \frac{z}{r}$

运动方程为

x = x(t), y = y(t), z = z(t)

$\bf{r} = \bf{r}(t)$

其中变量 t 就是运动时间啦，描述每个时刻，质点的位置，将变量 t 通过变换消去即可得到轨迹方程

例子

我现在有一个运动方程 $x = 3\sin{\frac{\pi}{6}}t$， $x = 3\cos{\frac{\pi}{6}}t$， $z = 0$

显然，他的轨迹是一个圆，但是如何得到一个圆的方程呢？

注意到 $\cos^2 + \sin^2 = 1$

那么不难发现，$x^2 + y^2 = 9$，这显然就是一个半径为 3 的圆的方程，并且 z 在这里没有任何作用，始终为 0，但是千万别漏写上了

完整的轨迹方程为

$x^2 + y^2 = 9$，$z = 0$

位移

在 Δt 的时间内，质点由 A 点移动到 B 点，A、B 两点的位矢分别记为$\bf{r_1}，\bf{r_2}$，则位矢增量为

$Δ\bf{r} = \bf{r_2} - \bf{r_1}$

位移大小只能记为 $|Δ\bf{r}|$，而不能是 Δr，因为 Δr 一般表示位矢大小的增量，也就是 Δr = $|\bf{r_2}| - |\bf{r_1}|$

通常，$|Δ\bf{r}| \ne Δr$，在 $Δt \to 0$ 时，才有 $|Δ\bf{r}| = ds$，但是仍没有 $|d\bf{r}| = dr$

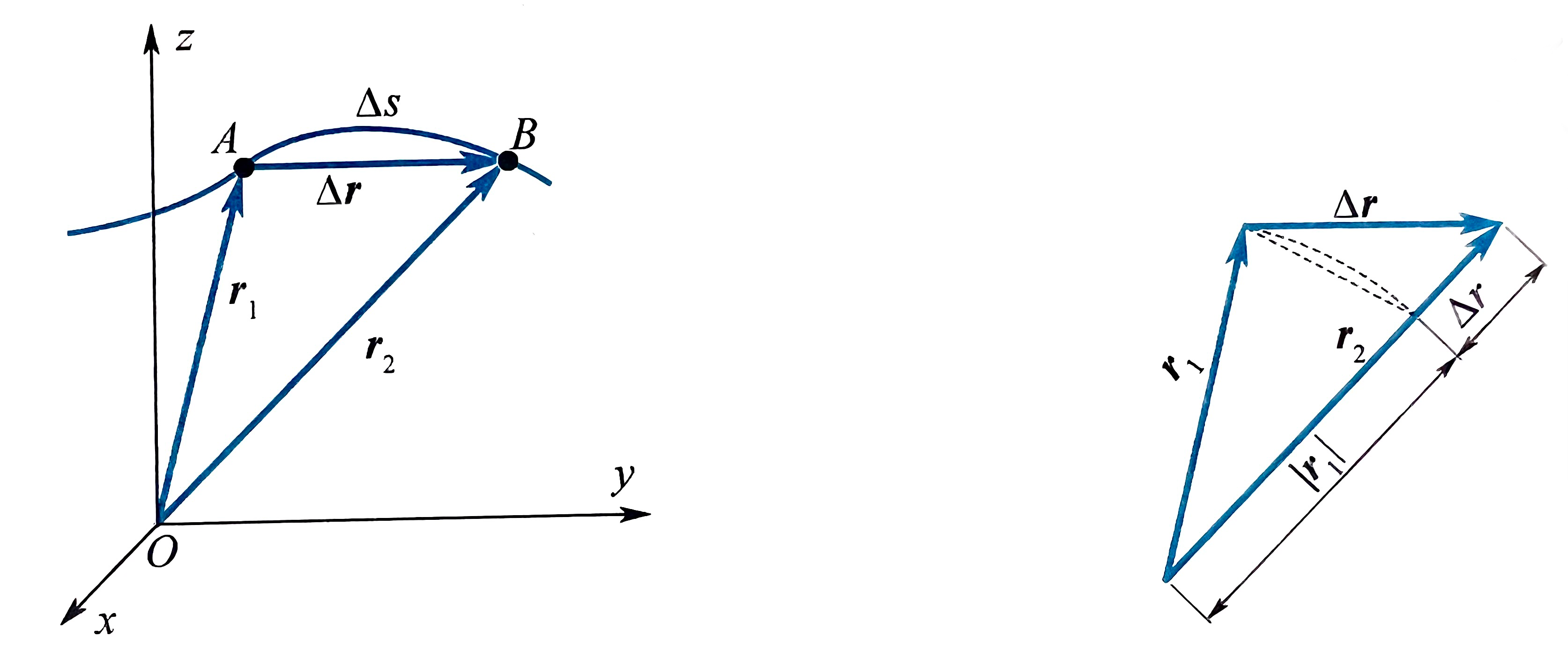
位移的模为

$|\bf{r}| = \sqrt{Δx^2 + Δy^2 + Δz^2}$

速度

$Δ\bf{r}$ 与 Δt 的比值称为质点在时刻 t 附近 Δt 时间内的平均速度

$\overline{\bf{v}} = \frac{\vec{AB}}{Δt} = \frac{Δ\bf{r}}{Δt}$

若变为微分形式，即变成了瞬时速度

$\bf{v} = \lim\limits_{Δt \to 0}\frac{Δ\bf{r}}{Δt} = \frac{d\bf{r}}{dt}$

即速度是位矢对时间的一阶导

速度也可以表示成

$\bf{v} = v_x\bf{i} + v_y\bf{j} + v_z\bf{k}$

模为

$|\bf{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}$

加速度

有了上面的基础，那么加速度在数学上就很好解释了，不就是速度的变化率吗，也就是速度对时间的一阶导，或者位矢对时间的二阶导

$\bf{a} = \frac{d\bf{v}}{dt} = \frac{d^2\bf{r}}{dt^2}$

也可以表示成

$\bf{a} = a_x\bf{i} + a_y\bf{j} + a_z\bf{k}$

模为

$|\bf{a}| = \sqrt{a_x^2 + a_y^2 + a_z^2}$

曲线运动的描述

来补习一下高等数学I(上)的内容，曲率

曲率的定义是

$k = \lim\limits_{Δt \to 0}\frac{Δ\theta}{Δs} = \frac{d\theta}{ds}$

曲率的公式是

$k = \frac{y^{''}}{(1 + (y^{'})^{2})^\frac{3}{2}}$

曲率半径

$ρ = \frac{1}{k} = \frac{ds}{d\theta}$

有了这个东西，我们就可以把曲线运动全部归结为局部的圆周运动，是不是好算多了

然后，我们又创建一种坐标系，自然坐标系，一条坐标轴朝运动方向切向，另外一条坐标轴法向，这时候，我们又可以把加速度分为两种，分别是法向加速度和切向加速度，一般记为$\bf{a}_n$ 和 $\bf{a}_\tau$，不难得出

$\bf{a} = \lim\limits_{Δt \to 0}\frac{Δ\bf{v}_\tau}{Δt} + \lim\limits_{Δt \to 0}\frac{Δ\bf{v}_n}{Δt} = \frac{dv}{dt}\bf{\tau}_0 + v\frac{d\theta}{dt}\bf{n}_0 = a_\tau\bf{\tau}_0 + a_n\bf{n}_0$

$|\bf{a}| = \sqrt{a_\tau^2 + a_n^2}$

并且不难理解，法向加速度只改变运动方向不改变速度大小，而切向加速度只改变速度大小不改变运动方向，并且还有

$\begin{cases} \bf{a}_\tau = \frac{dv}{dt}\bf{\tau}_0 = \frac{d^2s}{dt^2}\bf{\tau}_0 \\ \bf{a}_n = \frac{v^2}{ρ}\bf{n}_0 = \frac{v^2}{R}\bf{n}_0 \end{cases}$

与之前类似，我们还可以引入角速度和角加速度

$\omega = \frac{d\theta}{dt}$
$\alpha = \frac{d\omega}{dt} = \frac{d^2\theta}{dt^2}$

在匀角加速度运动中，有

$\begin{cases} \omega = \omega_0 + \alpha{t} \\ \theta = \theta_0 + \omega_0t + \frac{1}{2}\alpha{t}^2 \\ \omega^2 - \omega^2_0 = 2\alpha(\theta - \theta_0) \end{cases}$

并且还有以下关系

$\begin{cases} ds = Rd\theta \\ v = \frac{ds}{dt} = R\frac{d\theta}{dt} = R\omega \\ a_\tau = \frac{dv}{dt} = R\frac{d\omega}{dt} = R\alpha \\ a_n = \frac{v^2}{R} = \omega^2R \end{cases}$

事实上，角速度 $\omega$ 的方向是垂直圆面过圆心的，与半径遵循右手定则，并且有

$\bf{v} = \bf{\omega} \times \bf{r}$

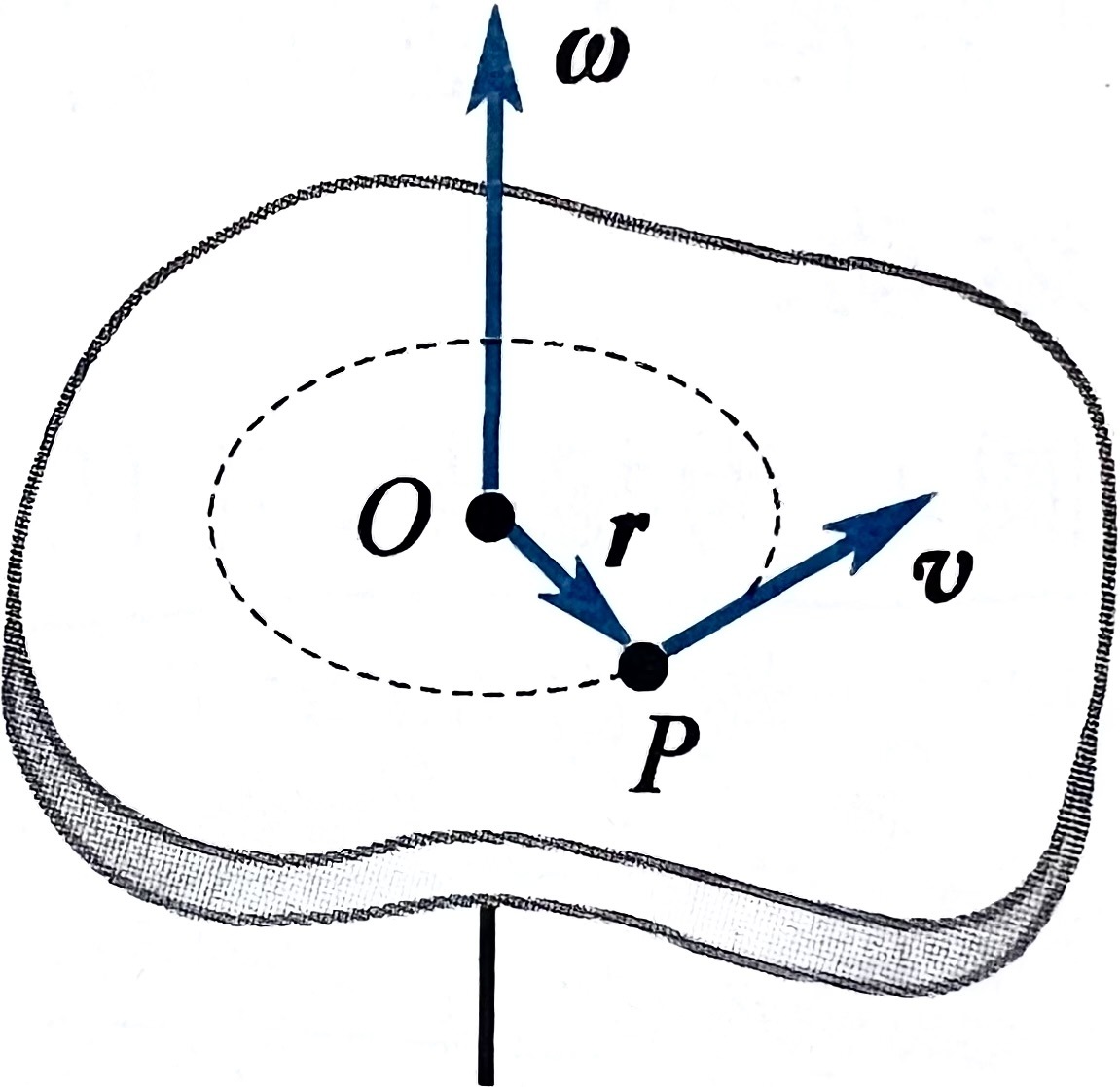
叉乘的运算法则

假设这里有两个向量

$\bf{\alpha} = (a, b, c)，\bf{\beta} = {d, e, f}$

则 $\bf{\alpha} \times \bf{\beta} = \begin{vmatrix} \bf{i} & \bf{j} & \bf{k} \\ a & b & c \\ d & e & f \end{vmatrix}$

$|\bf{\alpha} \times \bf{\beta}| = |\alpha||\beta|\sin\theta$

$\theta$ 为两个向量的夹角

相对运动

这还需要我讲吗？又不是洛伦兹变换，不懂的自己悟

例题

例1

如图所示，一个人用绳子拉着小车前进，小车位于高出绳端 h 的平台上，人的速率 $v_0$ 不变，求小车的速度和加速度的大小

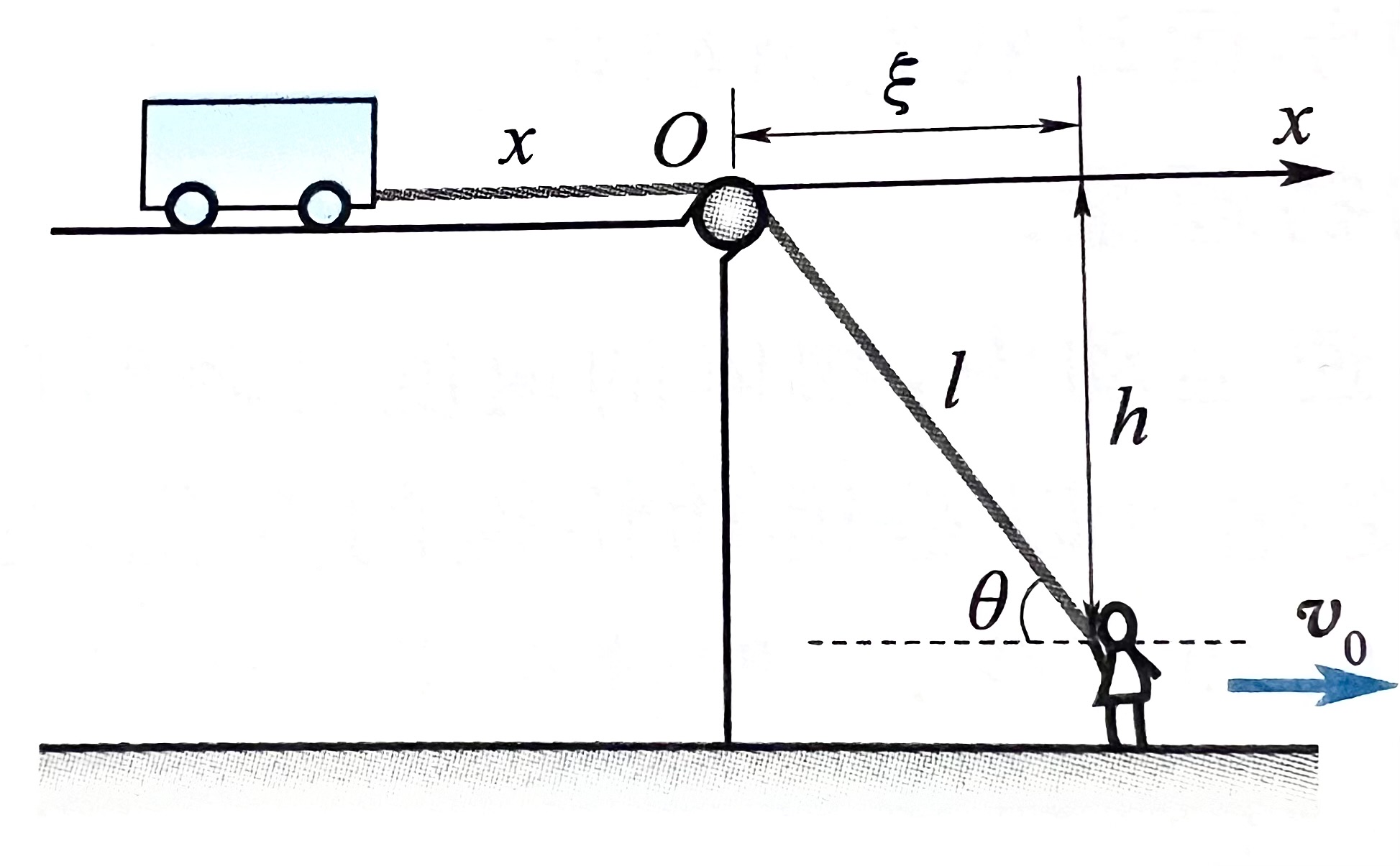
解

你会发现，这里头变化的有 $l、x、\xi$

一般来讲 $v_车 = \frac{dx}{dt}$ ，但是在这里你会发现你没办法找到比较直接的 $x$ 变化规律，但是你又发现，$x$ 和 $l$ 不是一起变的吗？而且变化的大小也一样，那不妨可以令

$v_车 = \frac{dl}{dt}$

那 $l$ 的变化规律呢？先别急，先看看一个初中就学了的公式：勾股定理

那你会发现

$l^2 = \xi^2 + h^2$

我们两边对 t 求导，其中 $x 和 l$ 与 t 有函数关系，h 是常量，于是求导后是

$2l\frac{dl}{dt} = 2\xi\frac{d\xi}{dt}$

$\frac{d\xi}{dt}$ 是啥？不就是 $v_0$ 吗？得到

$v_车 = \frac{dl}{dt} = \frac{\xi{v_0}}{l} = \frac{\xi{v_0}}{\sqrt{\xi^2+h^2}}$

那么加速度 $a = \frac{dv_车}{dt} = \frac{v_0^2h^2}{(\xi^2 + h^2)^\frac{3}{2}}$

$_{这个导怎么这么恶心人}$

例2

以速度 $\bf{v}_0$ 平抛小球，不计空气阻力，求 t 时刻小球的切向加速度的大小 $a_\tau$ 、法向加速度的大小 $a_n$ 和轨迹的曲率半径 $\rho$

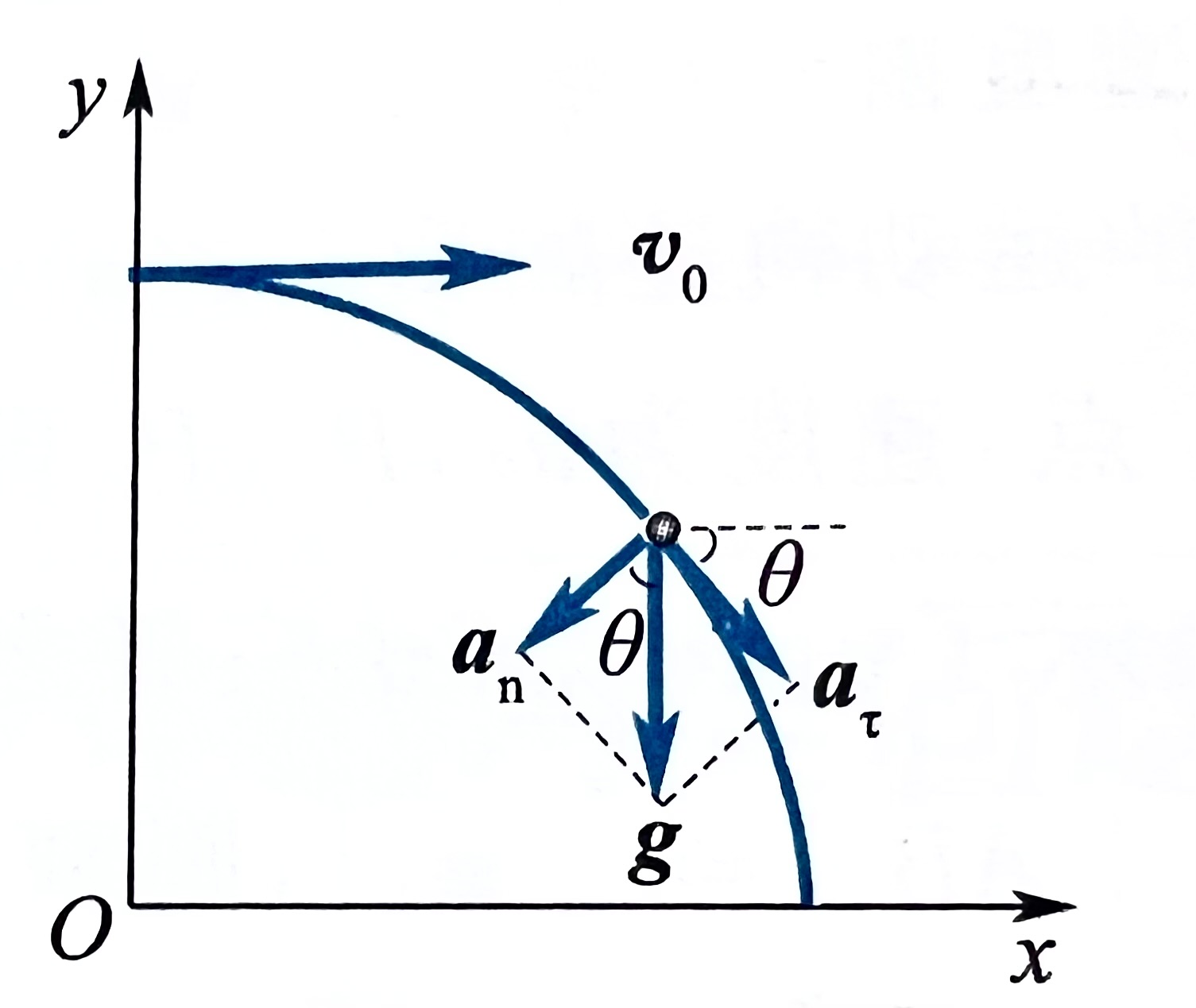
解

由图可知，$a_\tau = g\sin\theta$

但是，$\sin\theta$ 从何而来？你看一下运动轨迹，那么，它的速度，是不是始终都与轨迹相切？

因此，$\sin\theta = \frac{v_y}{v} = \frac{gt}{\sqrt{v_0^2 + g^2t^2}}$

于是，$a_\tau = \frac{g^2t}{\sqrt{v_0^2 + g^2t^2}}$

同理，$a_n = \frac{gv_0}{\sqrt{v_0^2 + g^2t^2}}$

关于 $\rho$，咱之前不是说过一个公式吗？$\bf{a}_n = \frac{v^2}{\rho}\bf{n}_0$，不妨变换一下

$\rho = \frac{v^2}{a_n} = \frac{v^2_x + v^2_y}{a_n} = \frac{(v^2_0 + g^2t^2)^\frac{3}{2}}{gv_0}$

这样就算出来了

例3

一质点做匀减速圆周运动，初始转速 n = 1500r/min，经 t = 50s 后静止。
（1）求角加速度$\alpha$和从开始到静止质点的转数 N
（2）求 t = 25s 时质点的角速度 $\omega$
（3）设圆的半径 R = 1m，求 t = 25s 时质点的速度和加速度的大小

解

(1)

n = 1500r/min = 3000$\pi$rad/min = 50$\pi$rad/s

则 $\alpha = \frac{0 - n}{t}$ = $-\pi$rad/$s^2$

求总共转过的 rad 数 $\theta = \theta_0 + \omega_0t + \frac{1}{2}\alpha{t^2}$，其中$\theta_0 = 0$，求得 $\theta = 1250\pi rad$

故总转数为 N = $\frac{1250\pi}{2\pi} = 625r$

(2)

显然，直接套公式 $\omega = \omega_0 + \alpha{t} = (50 - 25)rad/s = 25\pi{rad/s}$

(3)

由(2)，25s 时的质点速度 $v = R\omega \approx 78.5m/s$

则法向加速度 $a_n = R\omega^2 = \frac{v^2}{R} \approx 6.16 \times 10^3m/s^2$

切向加速度 $a_\tau = R\alpha \approx -3.14m/s^2$

例4

$一质点沿 x 轴移动，其加速度 a = -kv^2，式中 k 为正常数，设 t = 0 时，x = 0，v = v_0$
$（1）求 v 和 x 作为 t 的函数的表达式$
$（2）求 v 作为 x 的函数的表达式$

解

(1)

知，$a = -kv^2 = \frac{dv}{dt} \Rightarrow kdt = -\frac{1}{v^2}dv$

两边积分得到 $kt = \frac{1}{v} + C_1$

$令 t = 0，由此时 v = v_0，得 kt = \frac{1}{v} - \frac{1}{v_0}，整理得到 v = \frac{v_0}{1 + v_0kt}$

我们又知道 $dx = vdt，将 v 的表达式代入

$x = \int{\frac{v_0dt}{1 + v_0kt}} = \frac{1}{k}\ln{1 + kv_0t} + C_2$

同理，带入初始情况解得 $x = \frac{1}{k}\ln{1 + kv_0t}$

(2)

因为 $a = \frac{dv}{dt} = \frac{dv}{dx}\frac{dx}{dt} = v\frac{dv}{dx}$

因此不难得到 $\frac{vdv}{dx} = -kv^2$

步骤和 (1) 同理，我们可以得到 $v = v_0e^{-kx}$